What is the EROEI of a Renewables plus Hydrogen Energy System
New EROEI analysis of the Royal Society Large Scale Storage report from first principles
Introduction
The Royal Society published its Large-Scale Storage report (RS report) that concluded renewables plus hydrogen storage was a desirable solution to help the UK meet its 2050 Net Zero targets. I published an article that was critical of many aspects of the report. One of the criticisms was that the Energy Return on Energy Invested (EROEI) of the delivered system would be low. To illustrate this, the article used the proposed generation mix and the “buffered” EROEI figures from Weissbach et al to estimate the EROEI of the proposed system at around 3.8. I did note that the buffering approach assumed by Weissbach was pumped hydro and the proposed solution used hydrogen, so the properly measured EROEI would be different to that estimated.
This article tries to calculate the full-system EROEI from first principles. The EROEI of the renewables plus hydrogen solution must be lower than the weighted average of the renewables generation alone because the buffering or storage system adds more embedded input energy with no net extra energy output.
What is EROEI?
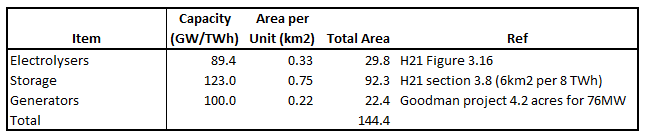
Simply speaking, the EROEI of an energy system is simply the ratio of the useful energy output from the system divided by the energy input required to create the system in the first place. For the Royal Society report, we might consider that we need to adjust the system boundaries to include the embedded energy required to build, accommodate and maintain the proposed 89.4GW of electrolysers; to create and maintain the 123TWh (LHV) of storage caverns and associated equipment including compressors and pipework and valves associated with hydrogen transmission system; and the energy required to build, accommodate and maintain the 100GW of generators used to burn the hydrogen.
We can calculate the EROEI of the whole system as follows:
EROEI = Eout / (Eig + Eis)
The EROEI of the system is the lifetime energy out (Eout) divided by the total input energy which is the sum of the input energy for the generators (Eig) and the storage system (Eis)
EROEI of the Generation System
Weissbach arrived at an EROEI for an onshore wind system of 16, using 1.5MW turbines and a load factor of 23%. I recently wrote an article updating Weissbach’s figures using a typical 4.2MW onshore Vestas machine and made an estimate for a 15MW offshore machine. This concluded that a reasonable estimate of current onshore wind EROEI is 17.7 and offshore about 12.2. Weissbach estimated of an EROEI of 3.9 for solar at Northern European latitudes. Using the generation mix proposed by the Royal Society of offshore wind 56%, onshore wind 24% and solar 20%, this gives a generation system EROEI of 11.9.
However, the Royal Society report proposed that 741TWh of renewable generation capacity would be required to deliver the annual demand of 570TWh. This is an overbuild factor of 1.3. Taking this into account, the EROEI of the generation part of the system falls to 9.1.
Output Energy and Input Energy for the Generation System
The Vestas Life Cycle Analysis (LCA) reports assume a life of 20 years for their wind turbines. This seems a reasonable estimate for the solar panels too.
The expected total useful output from the system is 570TWh per year multiplied by 20 years which gives a value for Eout above of 11,400TWh. Using the EROEI of 9.1 gives the energy input for the generation system, Eig above, of 11,400/9.1=1,250TWh.
We now need to estimate the input energy required for the storage system Eis. This includes the energy required to make the 89.4GW of electrolysers, drill the wells and form the 123TWh of salt caverns and build the 100GW of hydrogen generators they proposed. Adding this input energy to the 1.250TWh input energy above will allow us to estimate the EROEI of the whole energy system.
Input Energy for Electrolysers
Finding reliable sources for the input energy for the electrolysers is not straightforward. However, this paper by Ruggeri and Gomez-Camacho indicates 1,200GJ or 0.33GWh per MW of electrolyser capacity. Scaling this up to 89.4GW of electrolyser capacity gives 30TWh of input energy required to make the electrolysers if we assume a life of 20 years. This might be an optimistic estimate because the electrolyser stack may need to be replaced part way through the life.
Storage Cavern Input Energy
Estimating the energy required to drill the wells and form the storage caverns is not straightforward. However, this paper by Legarth and Saadat estimated the energy required to drill geothermal wells. For a well depth of 1,750m using a 17.5” bit size, this gives an energy requirement of 2GJ/m. This equates to 1GWh per well and assuming one well per cavern, which means also 1GWh per 300,000m3 cavern.
Each well will have to be cased with steel pipe. Assuming a 0.34m outer diameter with a 15mm wall thickness and a depth of 1,750m equates to 858 tonnes of steel per well. Using Weissbach’s 42Gj/t for high alloy steel equates to 10GWh of input energy for the steel casing per 300,000m3 cavern.
We now must calculate the energy required to pump seawater from the ocean down into the cavern, dissolve the salt and pump it back above ground and drain it back to the sea. Around 7-10 cubic metres of water are required to dissolve one cubic metre of salt. Using the high estimate to include the salt, a simple model of how much energy it takes to lift 10 tonnes of water through 1,750m, we can estimate the energy required per cubic metre of cavern at 47.7kWh. This calculation assumes that the gains from the hydrostatic pressure in the water as it goes down the well are balanced out by the head losses in pumping seawater from the ocean, down the well and back. This amounts to 14.3GWh for each 300,000m3 cavern.
Adding up all the different components gives 25.3GWh energy input per cavern. Each cavern of that size has a working volume of 144GWh of hydrogen (see H21 report p158), which equates to 0.18GWh of input energy per GWh hour of storage.
For 123TWh (LHV) of hydrogen storage, we therefore require 21.6TWh of input energy. The caverns may well have a life of more than 20 years. However, it is unlikely that the well casings, operating in high pressure hydrogen, will have a life longer than 20 years. In fact, the casing materials need to be chosen carefully to avoid hydrogen embrittlement. For the purposes of this calculation, I have assumed a life of 20 years for each cavern. Assuming a longer life will have the impact of reducing the input energy and increasing the whole system EROEI by a small amount.
Hydrogen Generator Input Energy
The Royal Society report assumes that hydrogen will be burned in four-stroke reciprocating engines. However, I cannot find data for the input energy required to make these devices. Weissbach provides data on the input energy required to build CCGT turbines, so for the purposes of this analysis, I have assumed CCGT gas-turbines are used to generate electricity from hydrogen instead.
Working through the data an assuming a pessimistic 20-year life, then the total input energy for 100GW of CCGTs burning hydrogen is 33TWh.
Hydrogen Transmission System
The RS report did not include any capex for a transmission system to connect the electrolysers, caverns and generators. The land requirements for the whole system are considerable as seen in Figure 1 below.
The location of the electrolysers will be governed by the availability of a secure and abundant water supply. The location of the storage caverns will be limited by geography to Cheshire, East Yorkshire and possibly Wessex. The generators could be almost anywhere. Even if it were technically possible to site all three elements close to each other, there will still be a requirement to join the components together with some sort of pipe network.
The H21 report assumed that 396km of 1,200mm high pressure pipe would be required for their hydrogen transmission system. Assuming a 15mm wall thickness this equates to 708,000 tonnes of steel which at 42GJ/t equates to 8.3TWh of input energy. I have assumed a similar sized network is required for the RS system.
Impact on Whole System EROEI
We now have a view of total input energy for the system. 1,250TWh (Eig) for the renewables generators, and Eis is the sum of 30TWh for the electrolysers, 21.6TWh for the storage caverns, 33TWh for the hydrogen generators and 8.3TWh for the hydrogen transmission system.
Plugging this into the equation above gives us an EROEI for the whole system of around 8.5.
What Might be Missing from the Calculation?
This result is higher than expected using a weighted average EROEI from Weissbach’s buffered values for wind and solar. So, the question arises are there any areas of input energy that might be missing. I can think of three potential areas:
Maintenance
Hydrogen compression, cooling and pumping losses
Energy required to build a dedicated reservoir.
The energy costs of annual maintenance of the storage system will be a fraction of the initial installation costs. Given the magnitude of the initial input energy, the energy costs of annual maintenance will make only a trivial difference to the calculations.
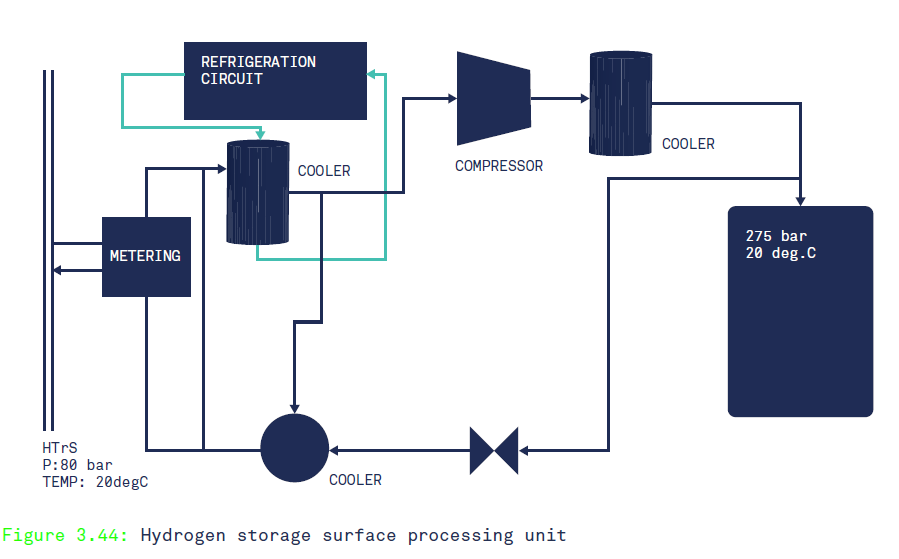
Assuming the hydrogen exits the electrolysers at around 30bar and then must be compressed up to the maximum pressure of the salt caverns around 275bar, the energy required to do this will be considerable, around 2.5-3% of the embedded energy in the hydrogen. The H21 report (p153) also shows that the hydrogen will need to be cooled in both the compression and expansion cycles, see Figure 2 below.
The RS report made no allowance for these losses. There is perhaps some potential to use the exhaust gasses from the hydrogen generators to further heat the hydrogen as it leaves the storage caverns and force it to do work during the expansion phase which will limit the losses.
However, for the purposes of this calculation, let us assume that overall compression, cooling and pumping losses of the hydrogen are around 5%. This would effectively reduce the useful output energy by 5%, reducing the full system EROEI to around 8.1.
The third area that may affect the calculation is if the electrolysers need a dedicated reservoir to secure a steady supply of fresh water. The energy density of hydrogen is 33.3kg/kg. Therefore, 123TWh of hydrogen would have a mass of 3.7m tonnes. Hydrogen makes up 11.1% of the mass of water, so the water required to completely fill the hydrogen storage would be 33.2m tonnes. This is about 40.2% of the size of Haweswater in the Lake District which can hold 84m tonnes of water. It took 1,500 million tonnes of concrete to make the dam for Haweswater. Scaling this down, a reservoir large enough to hold enough water to fill the hydrogen store would consume 604m tonnes of concrete. Again, using Weissbach’s material inventory, this would consume some 503TWh of energy. However, such a dam is likely to have a life of 100 years or more, so the input energy for the 20-year life would be ~100TWh. Adding this energy to the required input energy would result in an overall system EROEI of 7.5.
Conclusion
The method of calculating the full system EROEI using Weissbach’s buffered values gave a result of 3.8. It is likely that this approach was too pessimistic. Using the analysis in this article, it is fair to say that the full system EROEI for renewables plus hydrogen solution is in the range 7.5 to 8.5 as shown in Figure 3 below.
This is a better result, but given Weissbach also estimated the economic threshold to be 7, then a full system EROEI of 7.5-8.5 is not something to which we should aspire. It is certainly much lower than the EROEI of around 30 expected from gas and coal and a full order of magnitude lower than nuclear power plants with EROEI of around 75-100. Full-system EROEI is not a reason to build a renewables plus hydrogen energy system.
If you have enjoyed this article, please share it with your family, friends and colleagues and sign up to receive more content.





Your articles continue to demonstrate that the signalling of virtue is the most energy intensive activity on the planet right now.
Do we know of ANY MPs that can hold a reasoned conversation on EROEI?